Research

Simulation of metabolic networks

The origin and evolution of metabolism is an interesting field of research with many unsolved questions. Simulation approaches have proven to be helpful in explaining properties observed in real world metabolic reaction networks. We propose here a more complex and intuitive graph-based model combined with an artificial chemistry. Instead of differential equations, enzymes are represented as graph rewriting rules and reaction rates are derived from energy calculations of the involved metabolite graphs.

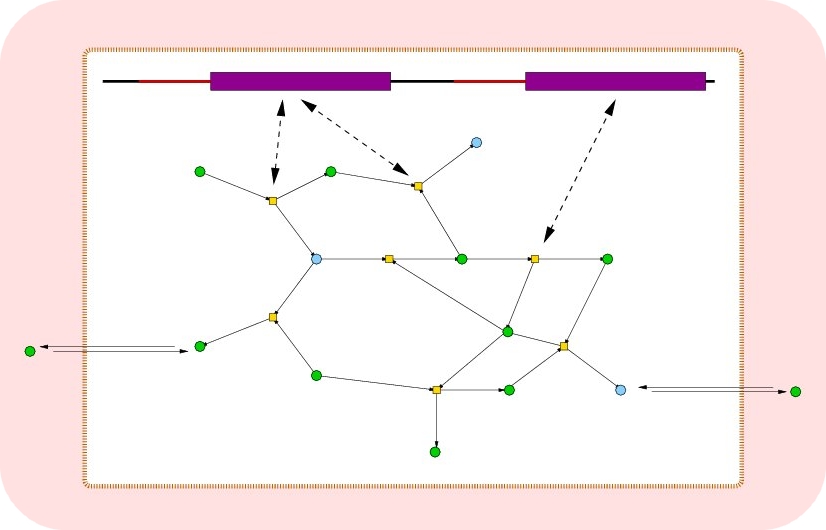
Initially, the environment (set of metabolites) and the chemistry (set of chemical reactions) are defined and a population of cells containing a genome and a (empty) metabolism are added to the simulation. The genes are expressed by mapping their RNA-sequence to an enzyme function. Enzymes look for reactants, produce new metabolites and thus build up the metabolic reaction network. In each generation, individuals are selected based on their metabolic yield and then create new individuals with mutated genomes.

Analysis of metabolic networks

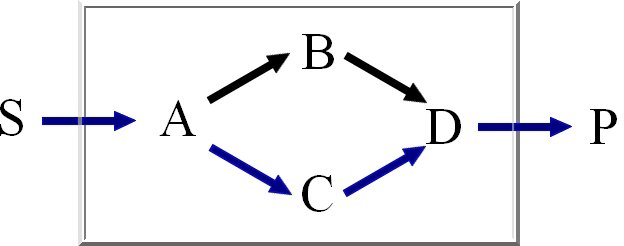
Metabolic pathway analysis is the calculation and analysis of the pathway distribution of a steadystate metabolic network to gain insights about its structure, functionality and properties. The calculation starts with the formation of the stoichiometric matrix presentation of the network and delivers the extreme pathways, spanning the entire steady state flux space, as the final result.

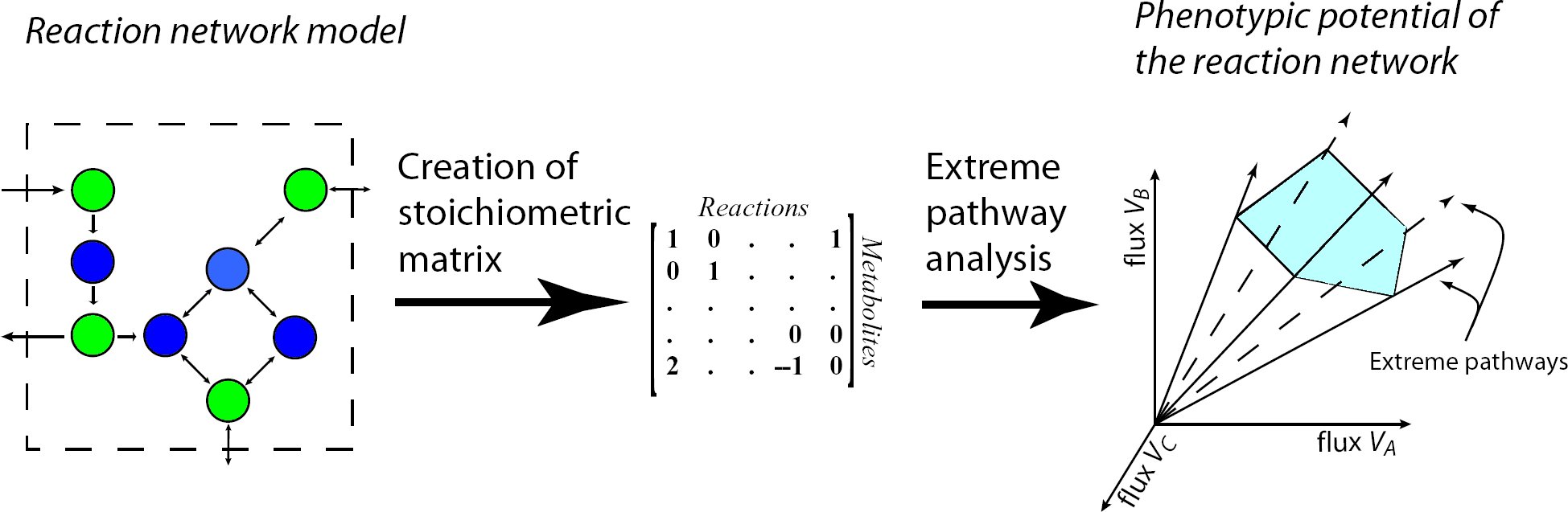
Extreme Pathways are the set of essential pathways through which all other possible pathways of the metabolic network can be generated, they are also minimal in the sense that they do not consist of smaller pathways.

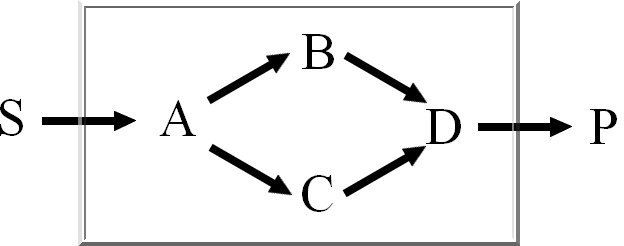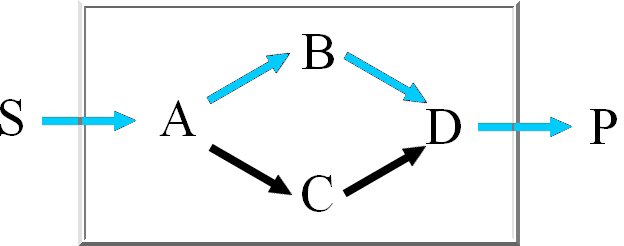
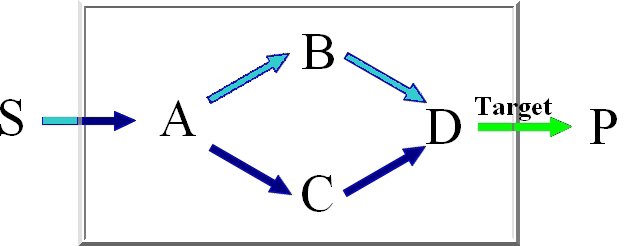
We calculate the set of extreme pathways with an improved binary Null-space approach. The computation time of the existing approach is dependent on the row-ordering. We integrated a new way to order the rows to reduce the number of candidate pathways.

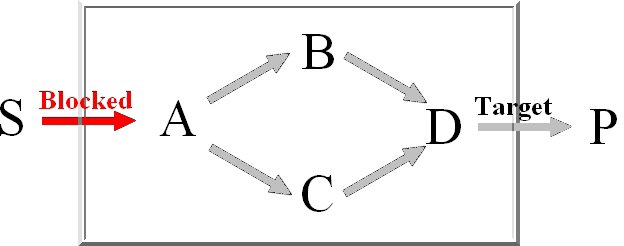
Minimal knockout sets are sets of reactions that need to be removed in order to disable the function of a certain target reaction, this means that there may not be any extreme pathway containing this target reaction.

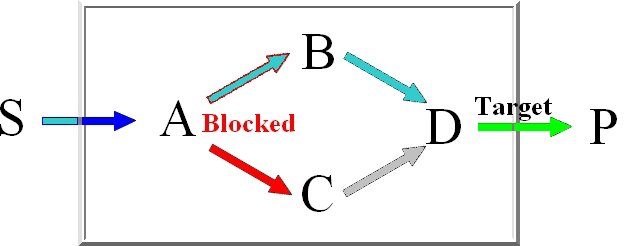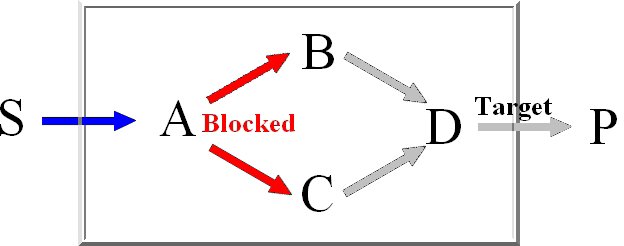
For the computation of the minimum knockout sets we implemented an improved depth-first version of Berge's algorithm which avoids the costly superset removal.

Emergence of network properties

The emergence and evolution of properties on the network level, is another intriguing question. Here we apply our metabolic pathway analysis tool to our simulation for the evolution of metabolisms. In this process the tool is used to define a realistic selection criteria -optimal metabolic yield- for the metabolisms, leading to networks with properties as observed in their real-world counterparts (e.g. scale free degree distribution). Further we use it to analyze less well understood properties of the resulting networks, such as robustness or modularity, to make predictions about their origin and development. It can also be used as a standalone tool for the enumeration of elementary modes and the subsequent computation of minimal cut-sets, in a very memory efficient way.

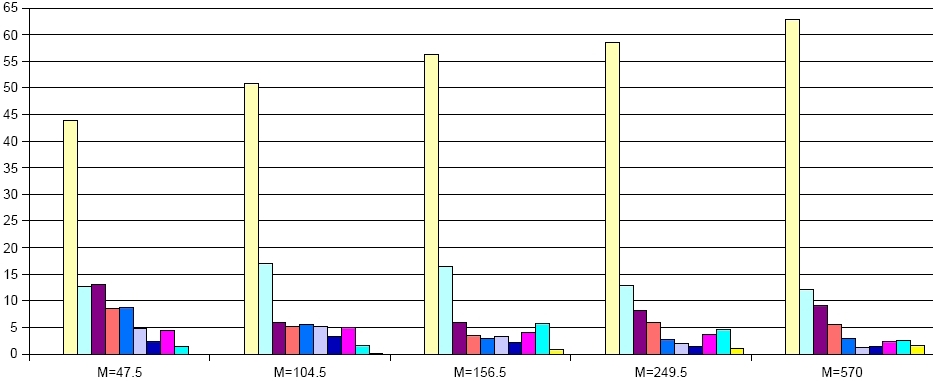
Robustness of a network can be defined as a property of the underlying graph structure or as a dynamical property of the system that is represented by the network. Simple graph-based measures for robustness are for example, degree or connectivity distributions, as well as the entropy. Measures for the robustness of the system dynamics, especially in metabolic networks, are related to fluxes through the system and their behavior to eleimination of edges (knockout of genes/enzymes) and nodes (depletion of metabolites). Here we use several measures based on the set of extreme pathways and the size distribution of the above described minimal knockout sets.

Genotype-Phenotype mappings

For many years it is known that neutral mutations have a considerable influence on the evolution in molecular systems. The folding of RNA sequences to secondary structures with its many-to-one property represents a mapping entailing considerable redundancy. Various extensive studies concerning RNA folding in the context of neutral theory yielded insights about properties of the structure space and the mapping itself. We intend to get a better understanding of some of these properties and especially of the evolution of RNA-molecules as well as their effect on the evolution of the entire molecular system.

We introduce a novel genotype-phenotype mapping based on the relation between RNA sequence and its secondary structure for the use in evolutionary studies. The inspiration for this particular mapping emerged from the modeling of RNA enzymes within our simulation framework for the evolution of metabolic reaction networks. The genome contains a number of RNA genes which then give rise to RNA enzymes acting on metabolites and thus shaping the metabolic network. The use of our mapping allows not only for a more realistic study of the evolution of the entire system, but also enables us to observe the behavior of our enzymes itself and therefore possibly gain some insights about the evolution of catalytic molecules in general.

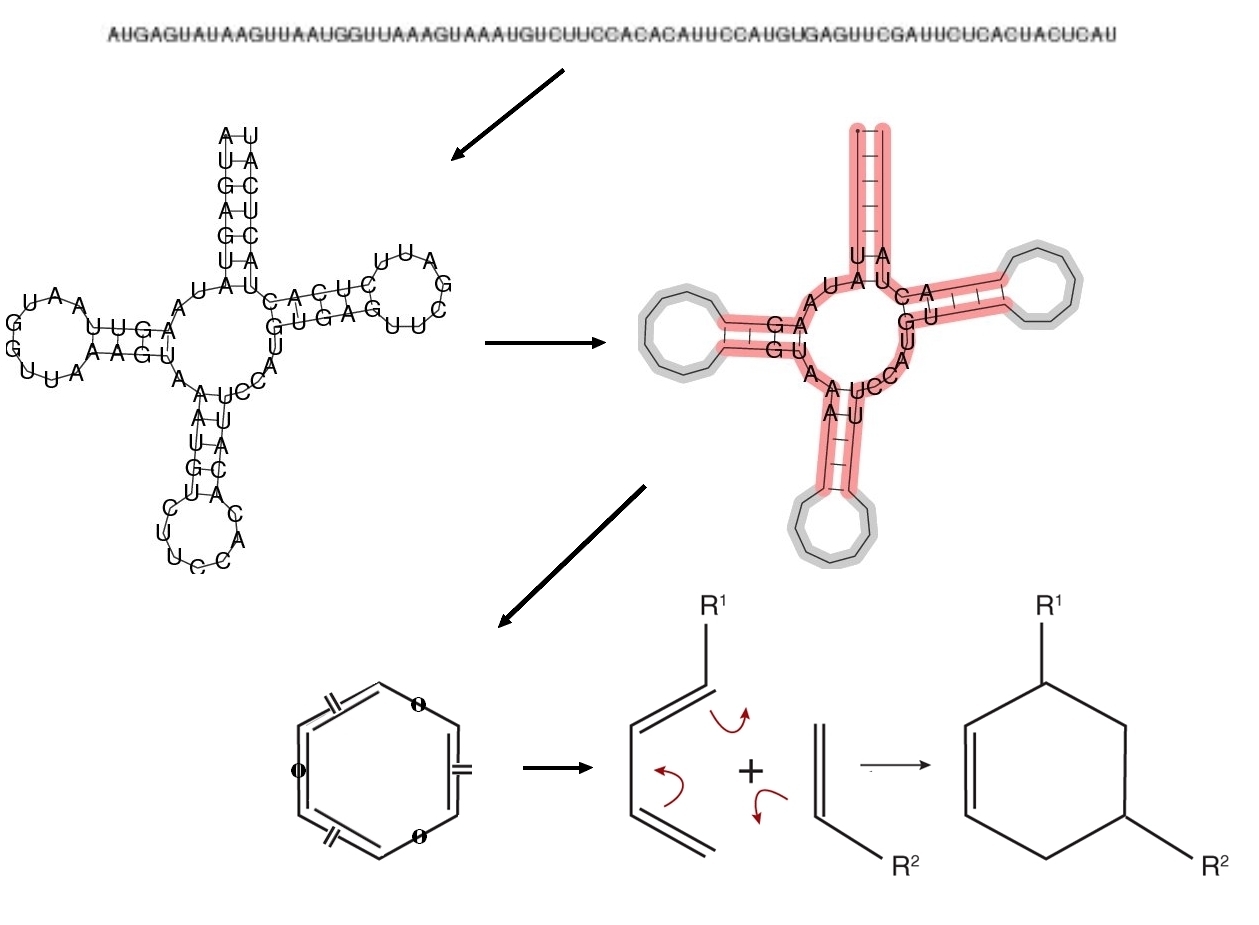
Enzymes typically have an active site where only few amino acids or bases determine its catalytic function and the remaining structure has mostly stabilization function. Accordingly, we extract structural and sequence information only from a restricted part of the fold. We decided to focus on the longest loop of the folded RNA. The idea for mapping the extracted information to a specific chemical reaction was encouraged by the fact that many enzymes catalyze a reaction by stabilizing its transition state. Recent work on hairpin ribozymes and other catalytic RNA support that as a common strategy for RNA enzymes. Given the definition of Fujita's imaginary transition structures (ITS), we developed a unique index for all possible pericyclic chemical reactions, describing the constitution of the reaction's transition state. Every RNA molecule is assigned such an reaction ID based on the information from its fold. The length of the longest loop specifies the number of involved atoms and the sequence within the loop determines the atom types. The bond types are derived from structural characteristics of the loop, such as the length and position of contained stems. Thus, a mapping from RNA sequence (genotype) to a chemical reaction (phenotype) is produced.

Besides using the mapping in several simulation runs which yielded realistic metabolic networks and connectivities, we performed several statistical tests commonly used in neutral theory, such as the number of visited phenotypes and the average discovery rate during a random neutral walk. We compared it with results of approaches using cellular automatons, random boolean networks and other mappings based on RNA folding. It exceeds all non-RNA mappings in extent and connectivity of the underlying neutral network. Further, it has a significantly higher evolvability and innovation rate than the rest. Especially interesting is the highly innovative starting phase in RNA-based mappings.

Protein function prediction

Predicting Function of proteins is an important problem in computational biology and many approaches have been introduced to solve this problem. However, there is no single approach which regards all issues of protein function prediction. The most promising clue to infer function seems to be Protein Packing Motifs, patterns of only a few amino acids which are spatially close together and possess similar bio-chemical and geometrical properties. Our approach finds these packing motifs by mining closed frequent subgraphs from a set of protein graphs. The key to finding good motifs is the use of optimal labels for nodes and edges of the protein graphs, thus we introduce a novel way to assign these labels based on credible biological characteristics of such motifs. The use of Feature Selection allows the approach to be extended with discriminative features other than our motifs. Possible additional features could come from other function prediction approaches. By assigning feature vectors to protein graphs we have the possibility to use our approach to develop a protein index for structural protein databases, in particular the PDB databse, since we extract all information for our approach solely from this database.

A packing motif is a pattern, representing a cluster of residues which are close in space with no restriction in sequence, e.g. distance or order, which occurs multiple times in a set of proteins. Due to that definition they can hardly be found by sequence analysis, thus our approach uses structural information. It is known that protein packing motifs can provide strong evidence for bio-chemical function, for example the function of the HIV virus was identified through a characteristic motif of this functional family.
Active sites of enzymes, which are also packing patterns, have usually different bio-chemical properties than the all other areas on the enzyme surface. For example ligand binding sites can be distinguished from other parts due to a high number of hydrophobic amino acids, which are mostly in the core of the protein rather than the surface. Other characteristics which can be used to detect such areas, are clusters of non-polar amino acids or certain combinations of polar amino acids. Considering this we decided to use these attributes to form the labels for the nodes in the protein graphs. We discarded the idea of using the amino acid type, because conservation in a packing motif means rather of a class than of a specific type.

Response network analysis

One important aspect of computational systems biology includes the identification and analysis of functional response networks within large biochemical networks. These functional response networks represent the response of a biological system under a particular experimental condition which can be used to pinpoint critical biological processes.

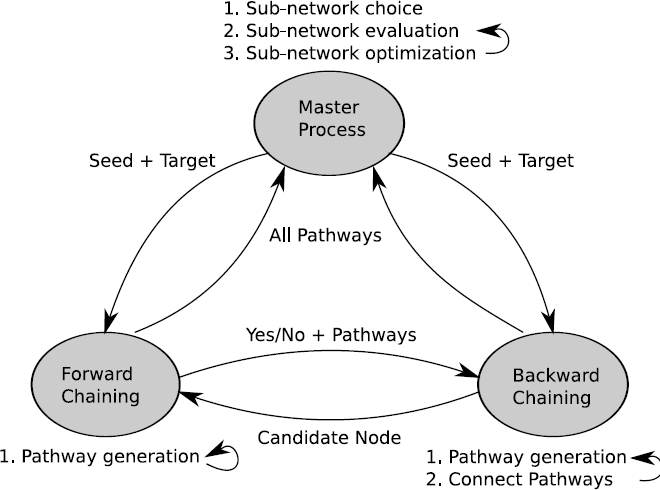
For this purpose, we have developed a novel algorithm to calculate response networks as scored/weighted sub-graphs spanned by k-shortest simple (loop free) paths. The k-shortest simple path algorithm is based on a forward/backward chaining approach synchronized between pairs of processors. The algorithm scales linear with the number of processors used. The algorithm implementation is using a Linux cluster platform, MPI lam and mpiJava messaging as well as the Java language for the application.

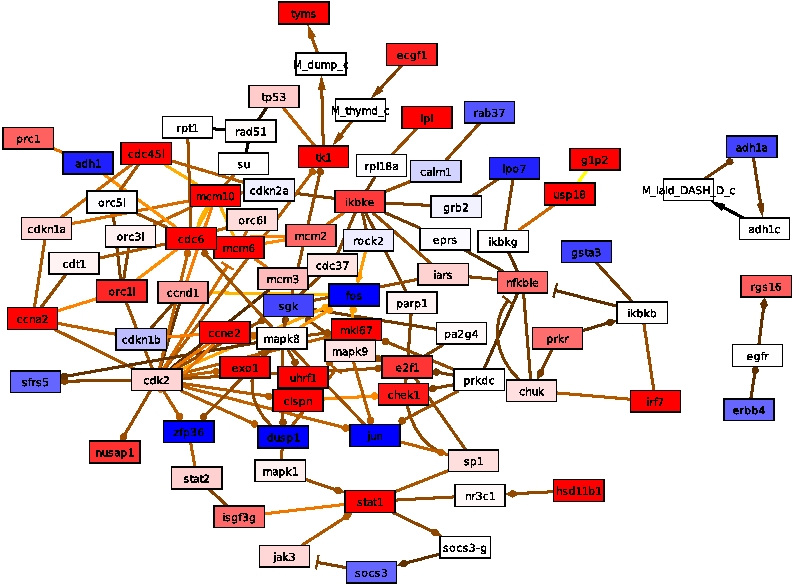
The algorithm is performed on a hybrid human network consisting of 45,041 nodes and 438,567 interactions together with gene expression information obtained from human cell-lines infected by influenza virus. Its response networks show the early innate immune response and virus triggered processes within human epithelial cells. Especially under the imminent threat of a pandemic caused by novel influenza strains, such as the current H1N1 strain, these analyses are crucial for a comprehensive understanding of molecular processes during early phases of infection. Such a systems level understanding may aid in the identification of therapeutic markers and in drug development for diagnosis and finally prevention of a potentially dangerous disease.